さて、オークスとダービーを前にして今回も謎のパズルです。

右の画像は、ある競馬のレースのオッズ表です。
ちょっと見づらいですが、よく見てください。このオッズにはある特徴…というか、ギャンブルとしてみた場合に大きな問題があります。それはなんでしょうか。
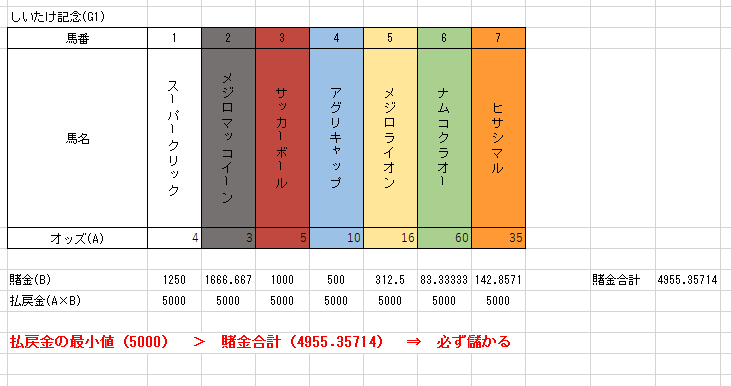
答えですが、右の画像のように1番の馬に掛け金を1250、2番の馬に1666.667、3番の馬に1000…と掛け金を賭けていった場合、賭金の合計は4955.35714となります(端数の表示が適当でスミマセン)。
一方で、どの馬が優勝しても払戻金(=オッズ×掛け金)として5000が手に入ります。
そう、このオッズには購入者側に必勝法があり、どの馬が強いのか弱いのか全く知らなくとも、この賭け方をすれば確実に儲かるのです。つまりギャンブルとして成立しないのです。
そういうオッズがあり得ること自体は容易に理解できます。例えば出走馬が2頭でオッズが共に3倍なら、誰でも儲けられるのは当たり前です。
ただ、ここで疑問がわきます。そのような必勝法があるオッズとないオッズの違いは何なのでしょうか。例えば片方の馬のオッズが1.2倍だとして、もう一方の馬のオッズがどのぐらい大きければ必勝法があるのでしょうか。そして馬が3頭以上ならどうでしょうか。どうやって必勝法の有無を判別できるでしょうか。

比較的単純な例として出走馬が3頭の場合で考えてみましょう。
オッズが右の画像のようなものであるとします。ここで「確実に1の払戻金が得られる賭け方」というものを考えてみます。
べつに難しくはありません。
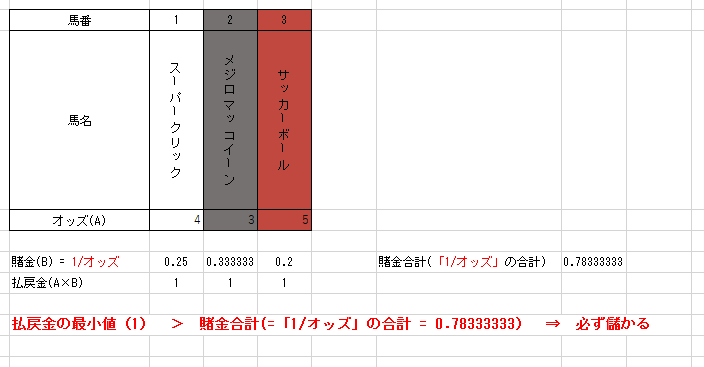
1番の馬のオッズが4倍ですから、その逆数つまり1/4=0.25を1番の馬に賭ければ、1番の馬が優勝したときに1の払戻金が得られます。
また、2番の馬のオッズが3倍ですから、その逆数つまり1/3=0.333333を2番の馬に賭ければ、2番の馬が優勝したときに1の払戻金が得られます。
また、3番の馬のオッズが5倍ですから、その逆数つまり1/5=0.2を3番の馬に賭ければ、3番の馬が優勝したときに1の払戻金が得られます。
以上の賭け方により、どの馬が優勝しても1の払戻金が手に入ります。これが「確実に1の払戻金が得られる賭け方」です。このときの賭金の合計はつまり「各出走馬のオッズの逆数の和」であり、この例では0.78333333となっています。
さて、もうお気づきのことと思います。「確実に1の払戻金が得られる賭け方」が必要とするコスト、つまり賭金の合計は「各出走馬のオッズの逆数の和」で表され、この場合はそれが0.78333333、つまり1に満たないなのです。
ですからこの賭け方自体が必ず儲かる賭け方になっています。その賭け方というのは「各馬のオッズの逆数に比例した賭金を賭ける」ことなのです。
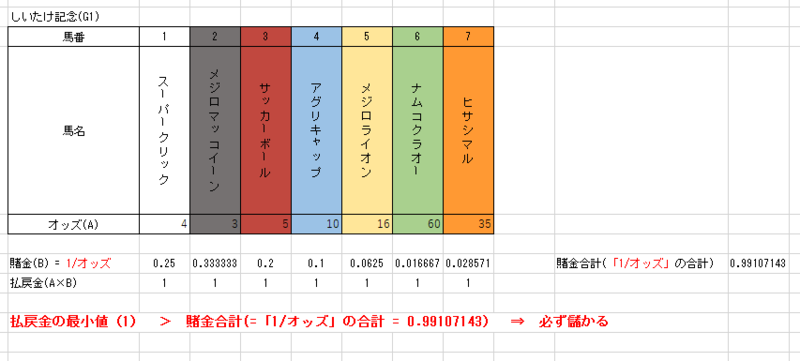
最初の例に戻って同じ考え方を適用してみます。
オッズの逆数を足し上げると、0.99107143となります。1に満たないので必ず儲かる賭け方があることがわかります。
2番目の画像で示した買い方は、この「確実に1の払戻金が得られる賭け方」を5000倍したものに過ぎません。
結論
オッズの逆数の和が1未満(以下)なら絶対に儲かる(損しない)賭け方が存在する
なお、現実のギャンブルでこのようなオッズにお目にかかることはありえません。また、上記のような賭け方をしても損するだけですのでお間違えのないよう_ _)