[※2022年11月追記] 新関数を使った総当たり法の例を別ブログに記載していますのでそちらもどうぞ。
松の内も明けたところで今年初の記事です。今年もよろしくお願いします。
さて、いきなりですが今日のテーマはナップサック問題の動的計画法による解決です。普通はVBAかソルバーでやるところですが、方法的にワークシート関数で実現できそうなのでやってみます。
問題の概要
ここで扱うのは「0-1ナップサック問題」で、詳細は次のとおりです。
- 価値、重量がそれぞれ異なるアイテムがいくつかあり、定められた上限重量以内で価値が最大になるようにアイテムを選択する
- 1つのアイテムを分割したり2回以上選択することはできない
- 重量は整数とする
動的計画法の適用については以下のサイトなどが参考になるかと思います。
正直難しいですが、各アイテムに順次着目しながら漸化式の要領で解いていくことができ、総当たり式と比べて計算量を大幅に削減できるのが特長です。
手順
シート構成
画像が小さくてスミマセンがEXCELシートです。

まずは次のような各欄を設けます。
入力部
上限重量入力欄……B4
アイテム価値/重量入力欄……B8:C17
出力部
価値総和表示欄……E4
個々のアイテムの要否判定表示欄……E8:E17
作業部
参照列欄……G8:G17
重量総和メモ(DP)欄……H8:W17
入力行が10行ですので設定できるアイテムは10個までです。
重量総和メモ(DP)欄が16列ですので指定できる上限重量の限界は15までです。
なお、H6:W6に記入されている0~15の値は計算に用いられますので必須です。
また、G7:W7(緑色)はこの解法に特有のダミー行(0番アイテム)です。
関数の入力
では関数を入力していきます。
まずは重量総和メモ(DP)欄からです。

W8セルに次のように入力し、それからH8:W17の範囲でコピーします。
H8セルで始めるのが普通かと思いますがこっちの方が解法の考え方が見えやすいかと思いました;-o-)
=MAX(W7,IF($C8>W$6,0,OFFSET(W7,0,-$C8)+$B8))
この式により、1つ上のアイテムまでの選択結果に基づき、当該アイテムを追加するのとしないのとどちらが価値が高いのかを判定しています。
当該アイテムの重量に応じて参照先が変わるようにOFFSET関数を用いていますが、参照先が表外に飛び出さないようにIF関数を用いています。
次に参照列欄です。
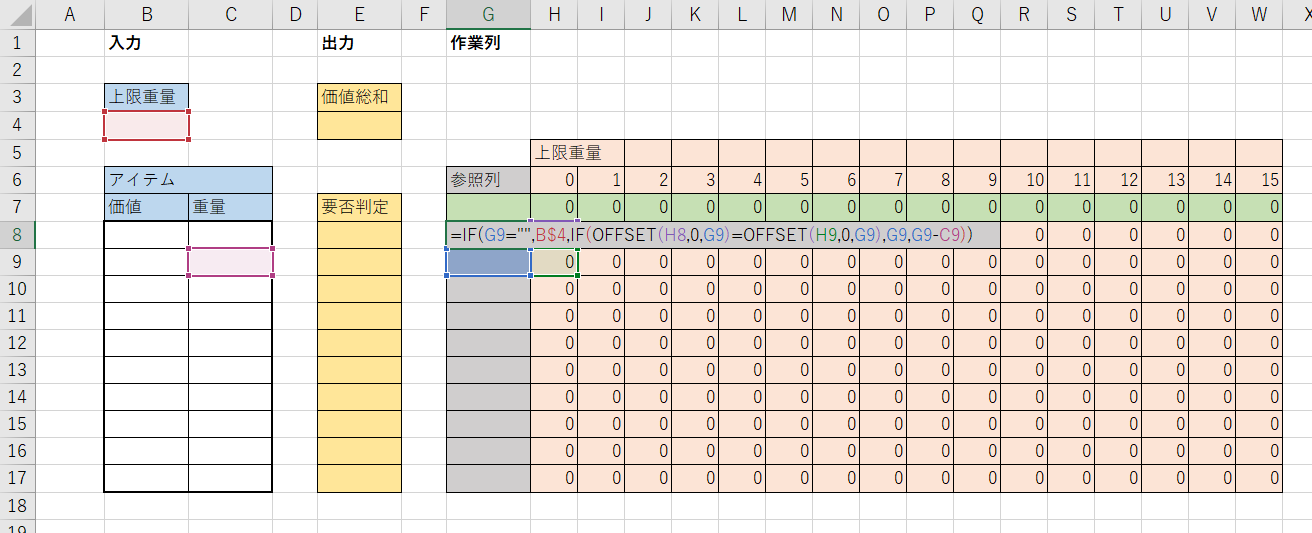
G8セルに次のように入力し、G17セルまでコピーします。
=IF(G9="",B$4,IF(OFFSET(H8,0,G9)=OFFSET(H9,0,G9),G9,G9-C9))
この欄の目的は、上記の選択の過程(最終結果につながるもの)を記録することです。結果を直接記録しているわけではありませんが、この値を1つ上の行と比較することにより判定することができます。
次に要否判定表示欄です。

E8セルに次のように入力し、E17セルまでコピーします。
=IF(OR(OFFSET(H8,0,G8)=0,G7=G8),"","○")
基本的に参照列欄の値が1つ上と同じであれば当該アイテムは選択されておらず、異なっていれば選択されているものと判定します。
複数の解(アイテム選択の組み合わせ)がある場合でも表示される組み合わせは1つのみです。
最後に価値総和表示欄です。

E4セルに次のように入力します。
=OFFSET(H7,COUNTIFS(B8:B17,"<>" & "",C8:C17,"<>" & ""),B4)
価値総和はSUMIFで求める方が簡単ですけども、あえて重量総和メモ(DP)欄からの表引きにしました。アイテムが記録されている行のうち最も下の行で、重量上限の値に対応する列の値が表示されます。
実行の様子
入力部に各アイテムの価値、重量を記入すれば解はリアルタイムに更新されます。
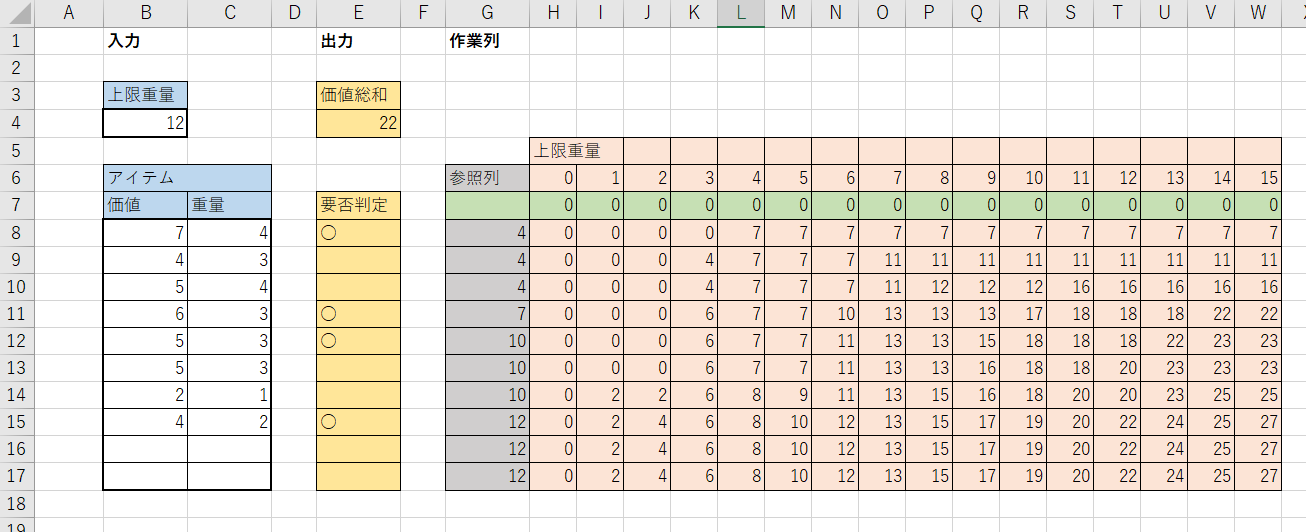
実際に値を入力した様子です。8つのアイテムデータと上限重量を入力したときの解が出力部に表示されています。
備考
上限アイテム数と指定できる上限重量の限界は、表をコピペで拡張することで容易に拡大できます。念のため上限アイテム数100(実際に100個設定)、上限重量の限界300でやってみましたところ、結果は上記の例と同様に一瞬で出ました(2018年春モデルのミドルレンジノートPC使用)。
方法的にアイテム数を増やすのは容易であるものの、個々のアイテム重量が4桁とか5桁とかになった場合に扱うのが難しい(列数不足、計算量増大に直結する)のが難点です。
結びになりますが、考え方は大きく間違っていないハズですけども酒漬けの年末年始に考えたものなのでなんか穴があるかもしれません。あしからず;-o-)